Matematik ve Eğlenceli dünyası

İNTEGRAL VE BELİRSİZ İNTEGRAL

İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x) fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latincetoplam kelimesinin ("summa") baş harfi s'nin biraz evrim geçirmiş hali olan ∫ işareti ile gösterilir. Bu işaret Leibniz tarafından tanımlanmıştır.

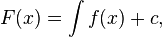
$F(x) = int f(x)+ c,$

c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.

Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamıdenir. İntegralin Riemann anlamındaki tanımı Riemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.

$S = lim_{Delta x to 0}sum_{i=0}^{n-1} f(x_i) Delta x_{i} = int_a^b f(x),dx = F(b)-F(a)$

Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x) göndermesinin integrali F(x) bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.

Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.

Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.

Köken Dilimize İngilizceden veya Fransızcadan geçmiş integral sözcüğü "bütüne ait olan" anlamına gelir ve İngilizceye Orta Fransızca intégral sözcüğünden; Orta Latince integralis (tüm yapmak, tümlemek) sözcüğünden; Latince integer (tüm, bütün, tam) sözcüğünden gelmiştir. Ayrıca integer sözcüğü tam sayı terimine karşılık olarak İngilizceye geçmiştir[1]. Türkçedetümlev sözcüğü, Osmanlıca mütemmem ile tamamî sözcüklerinin ve İngilizcedeki integral sözcüğünün anlamını karşılamak için türetilmiştir[2]. tümlev sözcüğü, "tümlenmiş şey" anlamına gelir. İsimden fiil yapan /-ev,-av/ yapım ekiyle kullanımda olan tümle[mek] fiilinden; isimden fiil yapan /-le[mek]/ yapım ekiyle muhtemelen Öz Türkçe *tüm (bknz. tümen) kökünden türetilmiştir.Osmanlıcada mütemmem sözcüğü kullanılmış (Arapçadaki *tm (tam) kökünden gelir) ancak Arapçada şu anda "olgun, evrimleşmiş, bütünleşmiş" anlamındaki tekâmül [3] sözcüğü kullanılmaktadır(kâmil, mükemmel, küme ile aynı kökten: *kml)[3].

İntegral alma yöntemleri

Değişken değiştirme

Basit fonksiyonların integrallari

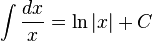
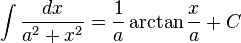
Rasyonel fonksiyonlar $int dx = x + C$ $int x^n,{rm d}x = frac{x^{n+1}}{n+1} + Cqquadmbox{ eğer }n ne -1$ $int {dx over x} = ln{left|xright|} + C$ $int {dx over {a^2+x^2}} = {1 over a}arctan {x over a} + C$

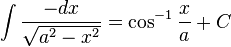
İrrasyonel fonksiyonlar $int {dx over sqrt{a^2-x^2}} = sin^{-1} {x over a} + C$ $int {-dx over sqrt{a^2-x^2}} = cos^{-1} {x over a} + C$ $int {dx over x sqrt{x^2-a^2}} = {1 over a} sec^{-1} {|x| over a} + C$

Logaritmik fonksiyonlar $int ln(x) ,dx = x ln(x) - x + C,$ $int log_b {x},dx = xlog_b {x} - xlog_b {e} + C$

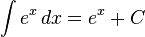
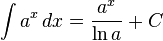
Üslü fonksiyonlar $int e^x,dx = e^x + C$ $int a^x,dx = frac{a^x}{ln{a}} + C$

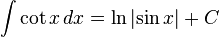
Trigonometrik fonksyionlar $int sin{x}, dx = -cos{x} + C$ $int cos{x}, dx = sin{x} + C$ $int tan{x} , dx = -ln{left| cos {x} right|} + C$ $int cot{x} , dx = ln{left| sin{x} right|} + C$ $int sec{x} , dx = ln{left| sec{x} + tan{x}right|} + C$ $int csc{x} , dx = ln{left| csc{x} - cot{x}right|} + C$ $int sec^2 x , dx = tan x + C$ $int csc^2 x , dx = -cot x + C$ $int sec{x} , tan{x} , dx = sec{x} + C$ $int csc{x} , cot{x} , dx = - csc{x} + C$ $int sin^2 x , dx = frac{1}{2}(x - sin x cos x) + C$ $int cos^2 x , dx = frac{1}{2}(x + sin x cos x) + C$ $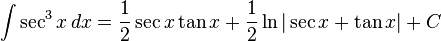int sec^3 x , dx = frac{1}{2}sec x tan x + frac{1}{2}ln|sec x + tan x| + C$ $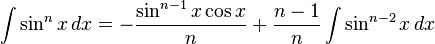int sin^n x , dx = - frac{sin^{n-1} {x} cos {x}}{n} + frac{n-1}{n} int sin^{n-2}{x} , dx$ $int cos^n x , dx = frac{cos^{n-1} {x} sin {x}}{n} + frac{n-1}{n} int cos^{n-2}{x} , dx$ $int arctan{x} , dx = x , arctan{x} - frac{1}{2} ln{left| 1 + x^2right|} + C$

Hiperbolik fonksiyonlar $int sinh x , dx = cosh x + C$ $int cosh x , dx = sinh x + C$ $int tanh x , dx = ln| cosh x | + C$ $int mbox{csch},x , dx = lnleft| tanh {x over2}right| + C$ $int mbox{sech},x , dx = arctan(sinh x) + C$ $int coth x , dx = ln| sinh x | + C$ $int mbox{sech}^2 x, dx = tanh x + C$

Ters hiperbolik fonksiyonlar $int operatorname{arcsinh} x , dx = x operatorname{arcsinh} x - sqrt{x^2+1} + C$ $int operatorname{arccosh} x , dx = x operatorname{arccosh} x - sqrt{x^2-1} + C$ $int operatorname{arctanh} x , dx = x operatorname{arctanh} x + frac{1}{2}log{(1-x^2)} + C$ $int operatorname{arccsch},x , dx = x operatorname{arccsch} x+ log{left[xleft(sqrt{1+frac{1}{x^2}} + 1right)right]} + C$ $int operatorname{arcsech},x , dx = x operatorname{arcsech} x- arctan{left(frac{x}{x-1}sqrt{frac{1-x}{1+x}}right)} + C$ $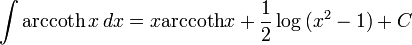int operatorname{arccoth},x , dx = x operatorname{arccoth} x+ frac{1}{2}log{(x^2-1)} + C$

İNTEGRAL İLE ALAN ARASINDAKİ İLİŞKİ

Aşağıdaki şekilde y = f(x) eğrisi y = g(x) eğrisi x = a ve x = b doğrusu arasında kalan taralı bölge verilmiştir.

Bölge (ya da eğriler) hangi konumda olursa olsun, yukarıdaki eğrinin denkleminden aşağıdaki eğrinin denkleminin çıkarılmasıyla oluşan belirli integral, bölgenin alanını ifade etmektedir

Bu sayfadan sonraki sayfada verilen şekilde x = f(y) eğrisi x = g(y) eğrisi y = a ve y = b doğrusu arasında kalan taralı bölge verilmiştir.

Bölge (ya da eğriler) hangi konumda olursa olsun, sağdaki eğrinin denkleminden soldaki eğrinin denkleminin çıkarılmasıyla oluşan belirli integral, bölgenin alanını ifade etmektedir.

Kural

1. Hangi konumda olursa olsun, alan daima pozitif bir reel sayı ile ifade edilir.

2. Belirli integralin değeri bir reel sayıdır.

3. İntegral ile alan ilişkilendirilirken, a. Alan x ekseninin üst kısmındaysa, alanı ifade eden sayı integrali de ifade eder.

b. Alan x ekseninin alt kısmındaysa, alanı ifade eden sayının toplama işlemine göre tersi integrali ifade eder.

Kural

y = f(x) parabolünün tepe noktasının apsisi r ordinatık; x = f(y) parabolünün tepe noktasının apsisi n ordinatı m dir.

Yukarıda solda verilen parabolde taralı alan,

Yukarıda sağda verilen parabolde taralı alan,

Yandaki şekilde y = f(x)fonksiyonunun grafiği verilmiştir. Taralı alan,

Bu kurallar bütün paraboller için geçerlidir.

Kural

Şekilde y = f(x) fonksiyonunun grafiği verilmiştir.

B. İNTEGRAL İLE HACİM ARASINDAKİ İLİŞKİ

Kural

y = f(x) eğrisi,

x = a, x = b doğruları ve x ekseni ile sınırlanan bölgenin (Taralı bölge) x ekseni etrafında 360° döndürülmesiyle oluşan dönel cismin hacmi:

Kural

x = g(y) eğrisi,

y = c, y = d ve y ekseni tarafından sınırlanan bölgenin (Taralı bölge) y ekseni etrafında 360° döndürülmesiyle oluşan dönel cismin hacmi:

Kural

y = g(x) eğrisi,

x = a, x = b ve y = f(x)tarafından sınırlanan bölgenin (Taralı bölge) x ekseni etrafında 360° döndürülmesiyle oluşan dönel cismin hacmi:

Kural

x = f(y) eğrisi,

y = c, y = d ve x = g(y) tarafından sınırlanan bölgenin (Taralı bölge) y ekseni etrafında 360° döndürülmesiyle oluşan dönel cismin hacmi:

A. DİFERANSİYEL KAVRAMIx in sonsuz küçük değişimi dx şeklinde gösterilir. Buna x değişkeninin diferansiyeli denir.

Fonksiyondaki değişim dy ile gösterilir.

D. İNTEGRAL ALMA YÖNTEMLERİ

1. Değişken Değiştirme Yöntemi

İntegrali alınan fonksiyon f(u)du gibi daha basit bir ifadeye dönüştürülerek integral alınır.

Kural

n ¹ –1 olmak üzere,

Kural

Kural

den başka köklü ifade içermeyen fonksiyonların integralini hesaplamak için, x = a × sint değişken değiştirmesi yapılır.

Kural

den başka köklü ifade içermeyen fonksiyonların integralini hesaplamak için,

değişken değiştirmesi yapılır.

Kural

den başka köklü ifade içermeyen fonksiyonların integralini hesaplamak için,

x = a × tant

değişken değiştirmesi yapılır.

Kural

köklü ifadelerini içeren fonksiyonların integrallerini hesaplamak için

E.k.o.k.(m, n) = p

olmak üzere,

ax + b = tp

değişken değiştirmesi yapılır.

2. Kısmî İntegrasyon Yöntemiu = f(x)

v = g(x)

olsun. u × v nin diferansiyeli,

d(u × v) = du × v + dv × u

olur. Buradan,

u × dv = d(u × v) – v × du

olur. Her iki tarafın integrali alınırsa,

Uyarı

Kısmî integralde u nun ve dv nin doğru seçilmesi çok önemlidir. Seçim doğru yapılmazsa, çözüme yaklaşmak yerine, çözümden uzaklaşılır.

Türev ve integral alma bilgileri ışığında, seçim sezgisel olarak yapılabilir. Ancak, kolaylık sağlayacağı için aşağıdaki kuralı göz önüne alabilirsiniz.

Kural

integrallerinde;

seçimi yapılır.

seçimi yapılır.

Sonuç

n bir doğal sayı olmak üzere,

f(x) bir polinom fonksiyon olmak üzere,

3. Basit Kesirlere Ayırma YöntemiP(x) ve Q(x) ortak çarpanı olmayan iki polinom olsun.

integrali, vereceğimiz iki yöntemden biriyle sonuçlandırılır.

a. P(x) in derecesi Q(x) in derecesinden büyük ya da eşit ise;

P(x) in derecesi Q(x) in derecesinden büyük ya da eşit ise P(x), Q(x) e bölünür.

b. P(x) in derecesi Q(x) in derecesinden küçük ise;P(x) in derecesi Q(x) in derecesinden küçükse ifade basit kesirlere ayrılır.

4. Trigonometrik Özdeşliklerden Yararlanarak İntegral Alma Yöntemi

Kural

dy = f '(x)dx ifadesine y = f(x) fonksiyonunun diferansiyeli denir.

2. Kısmî İntegrasyon Yöntemiu = f(x)

v = g(x)

olsun. u × v nin diferansiyeli,

d(u × v) = du × v + dv × u

olur. Buradan,

u × dv = d(u × v) – v × du

olur. Her iki tarafın integrali alınırsa,

Uyarı

Kısmî integralde u nun ve dv nin doğru seçilmesi çok önemlidir. Seçim doğru yapılmazsa, çözüme yaklaşmak yerine, çözümden uzaklaşılır.

Türev ve integral alma bilgileri ışığında, seçim sezgisel olarak yapılabilir. Ancak, kolaylık sağlayacağı için aşağıdaki kuralı göz önüne alabilirsiniz.

Kural

integrallerinde;

seçimi yapılır.

seçimi yapılır.

Sonuç

n bir doğal sayı olmak üzere,

f(x) bir polinom fonksiyon olmak üzere,

Matematik ve Eğlenceli dünyası

20 Mayıs 2012 Pazar

İNTEGRAL VE BELİRSİZ İNTEGRAL

1 yorum:

Blog Arşivi

İzleyiciler